테스트
Greedy Algorithm
Greedy 알고리즘의 개념
[ 개념 - Local Optimization Approach ]
지엽적인 방법을 가고 최적화된(라고 믿는)값을 선택하는 방법
• 일련의 선택들을 수행하며, 각 선택은 그 순간 가장 좋아 보이는 것을 선택함
• 각 선택은 국소적으로 최적일 수 있으나, 전역적으로 최적은 아닐 수 있음
[ 예시: Exchanges Greedy Algorithm ]
while (there are more coins and the instance is not solved){
grab the largest remaining coin; // selection procedure
if (adding the coin makes the change exceed the amount owed) // feasibility check
reject the coin;
else
add the coin to the change;
if (the total value of the change equals the amount owed) // solution check
the instance is solved;
}
| 최적의 방법 | 최적이 아닌 방법 |
|---|---|
탐욕 알고리즘의 적용 예시
이 글에서는
크루스칼 알고리즘,프림 알고리즘,다익스트라 알고리즘,스케줄링의 탐욕 알고리즘의 사용 예시를 다룬다!
참고 Minimum Spanning Tree(최소 신장 트리)
[ Undirected Graph ]
무방향 그래프 $G$는 유한한 정점 집합 $V(vertex)$과, 간선 집합 $E(edge)$로 구성
• 정점: $G$의 정점이라 불림
• 간선: 정점들의 쌍들로 구성된 집합, $G$의 간선이라고 부름
• 표기: $G = (V, E)$
예시
| 이미지 | 설명 |
|---|---|
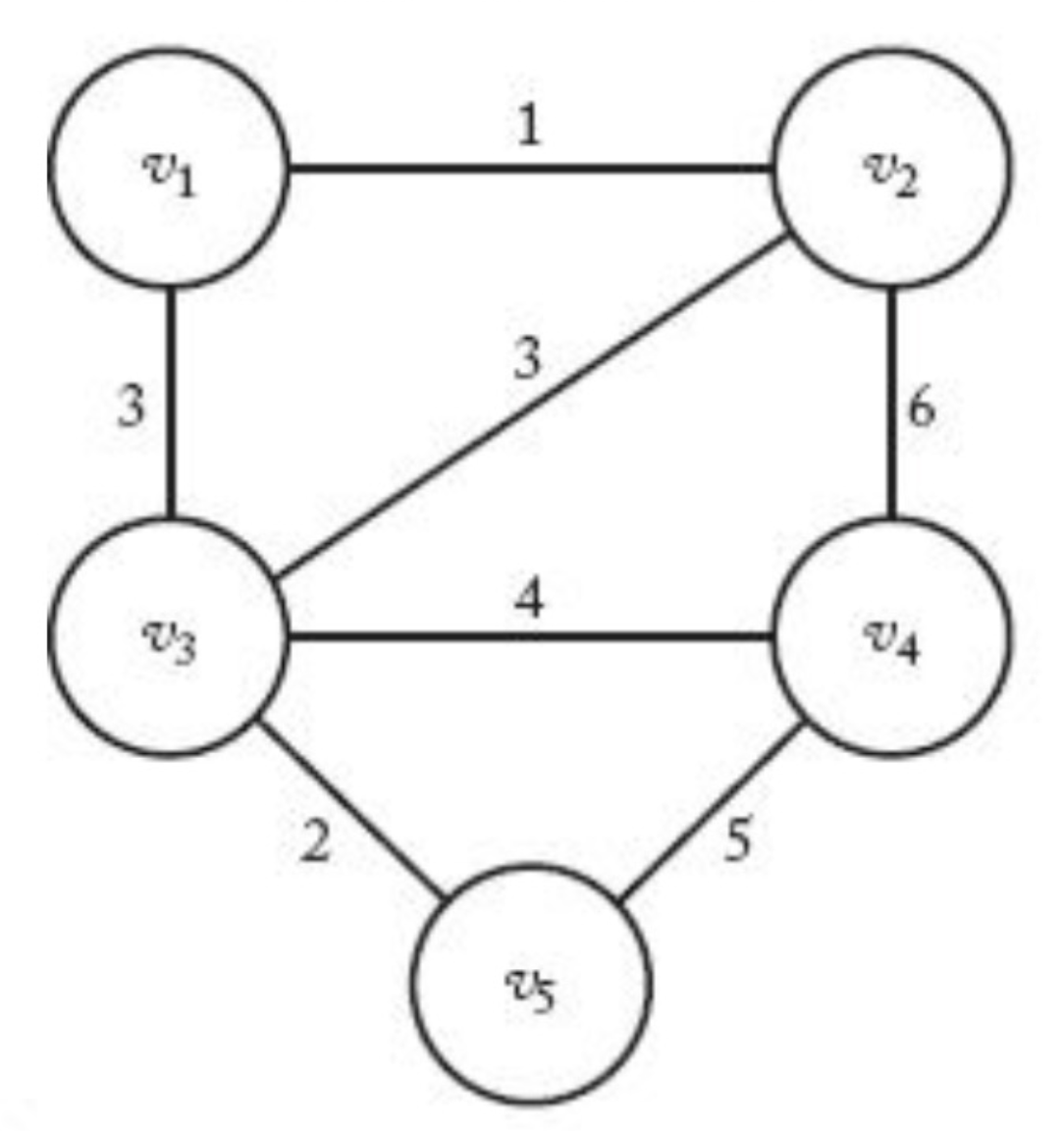 |
• $n(E) = 7$, $n(V) = 5$ • 직접적으로 연결된 노드: 이웃 • 그래프에는 순환은 있어서 트리는 아님 $V = \lbrace v_1, V_2, V_3, V_4, V_5\rbrace$ $E = \lbrace(V_1, V_2), (V_1, V_3), (V_2, V_3), (V_2, V_4), (V3, V_4), (V_3, V_5), (V_4, V_5)\rbrace$ |
[ Tree Structure ]
• 그래프에서 일부 엣지를 제거하여 순환 구조를 없애고 연결성을 유지한 서브그래프
• 트리는 모든 정점을 포함하고 사이클이 없는 연결된 구조
• 메시지 전파, 네트워크 연결 등에서 선호됨: 비용이 줄어듦
예시
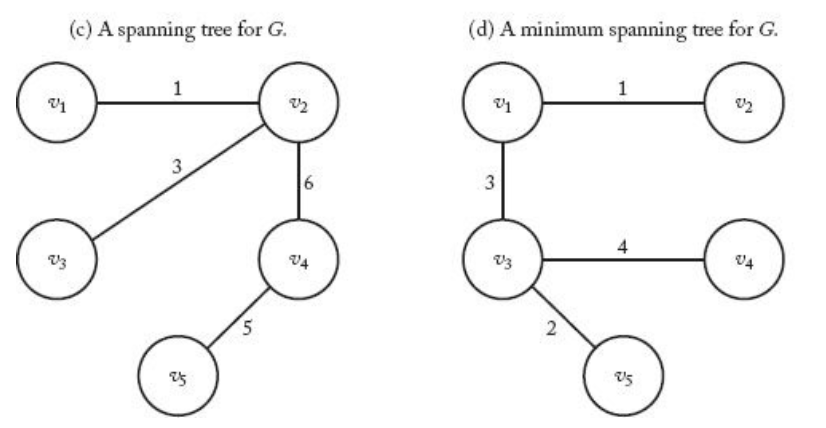
• (c) 스패닝 트리: weight = 15
• (d) 최소 스패닝 트리: weight = 10|
[ Minimum Spanning Tree ]
그래프 $G$의 모든 정점을 포함하고 연결된 부분 그래프이며 트리
• 최소 가중치를 갖는 연결된 부분 그래프는 스패닝 트리여야 함
• 하지만 모든 스패닝 트리가 최소 가중치를 가지는 것은 아님
F = ∅ // Initialize set of
// edges to empty
while (the instance is not solved){
select an edge according to some locally optimal consideration; // selection procedure
if (adding the edge to F does not create a cycle) // feasibility check
add it;
if (T = (V, F) is a spanning tree) // solution check
the instance is solved;
}
Prim’s Algorithm(프림 알고리즘)
[ 프림 알고리즘의 개요 ]
1) 그래프로 프림 알고리즘의 진행과정 알아보기
| 단계별 이미지 | 설명 | 집합 |
|---|---|---|
 |
최소신장트리 결정하기 | $V=\lbrace v_1, v_2, v_3, v_4, v_5\rbrace$, $Y=\lbrace \rbrace$ |
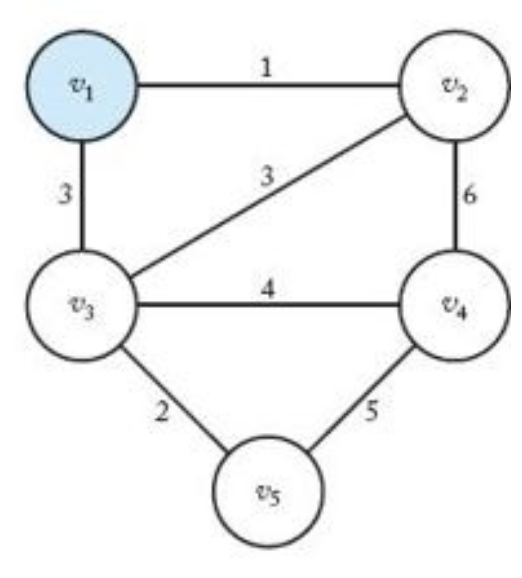 |
정점 $v_1$ 선택 | $Y=\lbrace v_1\rbrace$, $V-Y=\lbrace v_2, v_3, v_4, v_5\rbrace$ |
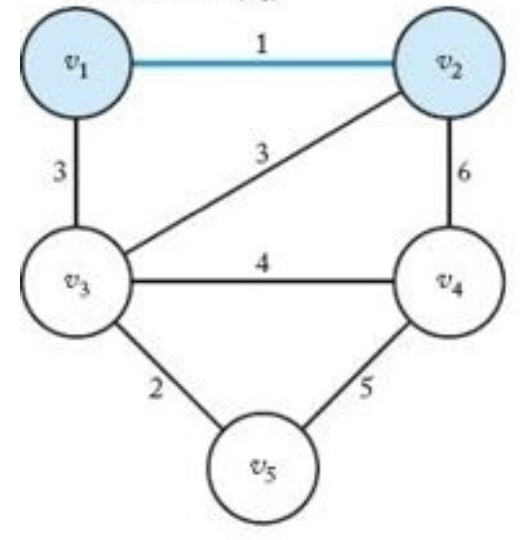 |
정점 $v_2$ 선택(정점 $v_1$ 의 이웃이므로) | $Y=\lbrace v_1, v_2\ rbrace$, $V-Y=\lbrace v_3, v_4, v_5\rbrace$ |
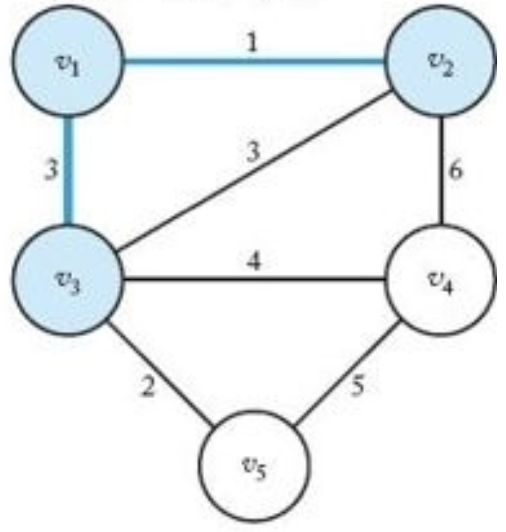 |
정점 $v_3$ 선택($\lbrace v_1, v_2\rbrace$ 의 이웃이므로) | $Y=\lbrace v_1, v_2, v_3\rbrace$, $V-Y=\lbrace v_4, v_5\rbrace$ |
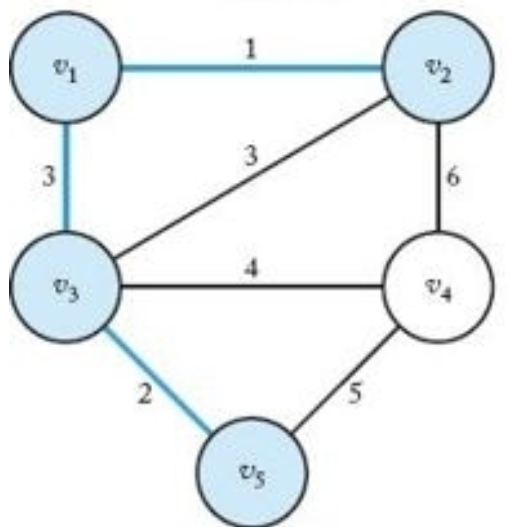 |
정점 $v_5$ 선택($\lbrace v_1, v_2, v_3\rbrace$ 의 이웃이므로) | $Y=\lbrace v_1, v_2, v_3, v_5\rbrace$, $V-Y=\lbrace v_4\rbrace$ |
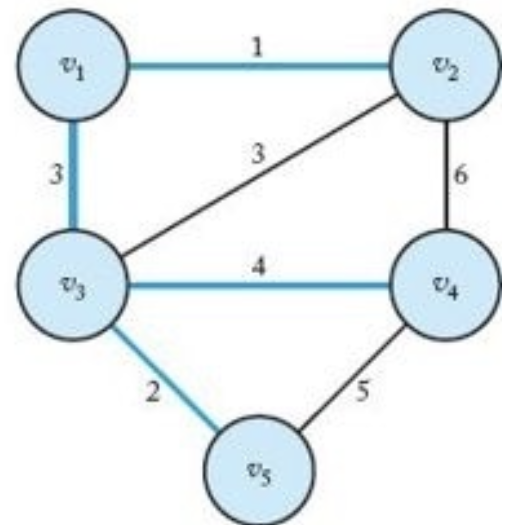 |
정점 $v_4$ 선택 | $Y=\lbrace v_1, v_2, v_3, v_4, v_5\rbrace$, $V-Y=\lbrace \rbrace$ |
2) 가중치 그래프를 인접행렬로 표현하기
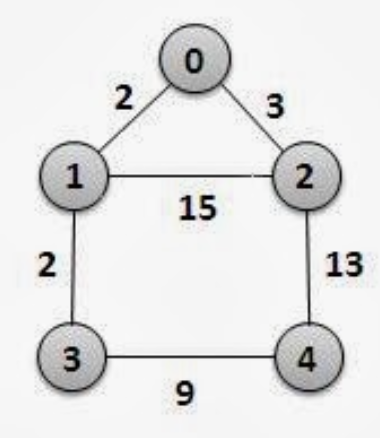
int adjacency_matrix[][] =
{
[0][2][3][∞][∞]
[2][0][15][2][∞]
[3][15][0][0][13]
[0][2][∞][∞][9]
[0][0][13][9][0]
}
3) 프림 알고리즘의 개요
F = ∅; // Initialize set of edges to empty.
Y = {u1}; // Initialize set of vertices to contain only the first one.
while (the instance is not solved){
select a vertex in V – Y that is nearest to Y; // selection procedure
add the vertex to Y;
add the edge to F;
if (Y == V) // solution check
the instance is solved;
}
[ 의사코드 및 실행예시 ]
void prim (int n,
const number W[][],
set_of_edges F)
{
index i, k, vnear;
number min;
edge e;
index nearest[2..n];
number distance[2..n];
F = ∅;
for (i = 2; i <= n; i++) {
nearest[i] = 1; // 모든 정점에 대해 u1을 가장 가까운 정점으로 초기화
distance[i] = W[1][i]; // Y에서 i까지의 거리를 가중치로 초기화
}
repeat (n − 1 times) { // Y에 n−1개의 정점을 추가
min = ∞;
for (i = 2; i <= n; i++) { // 모든 정점에 대해
if (0 ≤ distance[i] < min) { // Y에 포함되지 않은 정점 중 최소 거리 선택
min = distance[i]; // 최소값 갱신
vnear = i;
}
}
e = edge connecting vertices indexed
by vnear and nearest[vnear]; // vnear와 가장 가까운 정점을 연결하는 간선 e
add e to F; // e를 F에 추가
distance[vnear] = −1; // vnear를 Y에 추가했음을 표시
for (i = 2; i <= n; i++) { // Y에 포함되지 않은 정점들에 대해
if (W[i][vnear] < distance[i]) { // vnear를 거쳐가는 거리가 더 짧다면
distance[i] = W[i][vnear]; // 거리 갱신
nearest[i] = vnear; // 가장 가까운 정점 갱신
}
}
}
}

| W | $v_1$ | $v_2$ | $v_3$ | $v_4$ | $v_5$ |
|---|---|---|---|---|---|
| $v_1$ | 0 | 1 | 3 | ∞ | ∞ |
| $v_2$ | 1 | 0 | 3 | 6 | ∞ |
| $v_3$ | 3 | 3 | 0 | 4 | 2 |
| $v_4$ | ∞ | 6 | 4 | 0 | 5 |
| $v_5$ | ∞ | 6 | 4 | 5 | 0 |
| nearest | $v_n$에 연결된 노드 중 짧은 것의 번호 | 1 | 1 | 1>2>3 | 1>3 |
| distance | 가중치 | 1>-1 | 3>-1 | ∞>6>4>-1 | ∞>2>-1 |
[ 수학적 증명 ]
프림 알고리즘은 항상 최소 신장 트리를 생성
증명: 반복 루프의 각 단계 이후 간선 집합 F가 유망하다는 것을 수학적 귀납법으로 증명
1) 기초 단계 (Induction base)
초기 상태인 공집합 F는 유망
2) 귀납 가정 (Induction hypothesis)
반복 루프의 어떤 단계 이후, 현재까지 선택된 간선 집합 F가 유망하다고 가정
3) 귀납 단계 (Induction step)
• 다음 단계에서 선택될 간선 e가 F ∪ {e}를 여전히 유망하게 만듦을 보여야 함
• 선택된 간선 e는 Y와 V - Y를 연결하는 간선 중 가중치가 가장 작은 간선
• 따라서 F ∪ {e}는 여전히 유망한 최소 신장 트리의 부분 집합
결론 반복 루프가 끝난 후의 F는 하나의 최소 신장 트리가 됨
참고 Disjoint Set
[ 정의 ]
• 여러 원소가 있을 때, 이들을 서로 겹치지 않는 집합(분리 집합)으로 관리하는 자료구조
• 대표적인 용도: 크루스칼 알고리즘에서 사이클을 방지할 때 사용
[ 주요연산 ]
makeset
• Universal Set: $U = \lbrace A, B, C, D, E \rbrace$-> Sub set: $\lbrace a \rbrace$, $\lbrace b \rbrace$ …
각 원소 x를 자기 자신만 포함하는 하나의 독립 집합으로 초기화
for (each x ∈ U) makeset(x)
• 트리로 표현하면, 각 노드는 자기 자신을 부모로 가리킴
find with set_pointer p or q
• 원소 x가 속한 집합의 대표자(root) 찾기
• 보통 트리의 루트를 반환
merge(union)
• x와 y가 속한 서로 다른 두 집합을 하나로 합치는 연산
• find(x)와 find(y)로 각각 루트를 찾은 뒤, 한쪽 트리를 다른 쪽에 붙임
[ 예시 ]
[ 시간복잡도 ]
• initial make set:
[ 의사코드 ]
1) Disjoint Set의 기본구현 형태
const int n = // universe의 원소 개수;
typedef int index;
typedef index set_pointer;
typedef index universe[1..n]; // universe는 1부터 n까지 인덱싱
universe U;
void makeset(index i) {
U[i] = i;
}
set_pointer find(index i) {
index j;
j = i;
while (U[j] != j)
j = U[j];
return j;
}
void merge(set_pointer p, set_pointer q) {
if (p < q)
U[q] = p; // p가 병합된 집합을 가리킴
else
U[p] = q; // q가 병합된 집합을 가리킴
}
bool equal(set_pointer p, set_pointer q) {
if (p == q)
return true;
else
return false;
}
void initial(int n) {
index i;
for (i = 1; i <= n; i++)
makeset(i);
}
문제점: skewed tree
2) Disjoint Set Data Structure II (depth 기반 병합)
const int n = // universe의 원소 개수;
typedef int index;
typedef index set_pointer;
struct nodetype {
index parent;
int depth;
};
typedef nodetype universe[1..n];
universe U;
void makeset(index i) {
U[i].parent = i;
U[i].depth = 0;
}
set_pointer find(index i) {
index j;
j = i;
while (U[j].parent != j)
j = U[j].parent;
return j;
}
void merge(set_pointer p, set_pointer q) {
if (U[p].depth == U[q].depth) {
U[p].depth = U[p].depth + 1;
U[q].parent = p;
}
else if (U[p].depth < U[q].depth) {
U[p].parent = q;
}
else {
U[q].parent = p;
}
}
bool equal(set_pointer p, set_pointer q) {
if (p == q)
return true;
else
return false;
}
void initial(int n) {
index i;
for (i = 1; i <= n; i++)
makeset(i);
}
3) Disjoint Set Data Structure III (depth + smallest index 추적)
const int n = // universe의 원소 개수;
typedef int index;
typedef index set_pointer;
struct nodetype {
index parent;
int depth;
int smallest;
};
typedef nodetype universe[1..n];
universe U;
void makeset(index i) {
U[i].parent = i;
U[i].depth = 0;
U[i].smallest = i;
}
void merge(set_pointer p, set_pointer q) {
if (U[p].depth == U[q].depth) {
U[p].depth = U[p].depth + 1;
U[q].parent = p;
if (U[q].smallest < U[p].smallest)
U[p].smallest = U[q].smallest;
}
else if (U[p].depth < U[q].depth) {
U[p].parent = q;
if (U[p].smallest < U[q].smallest)
U[q].smallest = U[p].smallest;
}
else {
U[q].parent = p;
if (U[q].smallest < U[p].smallest)
U[p].smallest = U[q].smallest;
}
}
int small(set_pointer p) {
return U[p].smallest;
}
Kruskal Algorithm (크루스칼 알고리즘)
[ Kruskal 알고리즘이란 ]
정의
최소 신장 트리(MST, Minimum Spanning Tree)를 구하는 대표적인 Greedy Algorithm(탐욕 알고리즘)
• 그래프의 모든 정점을 최소한의 간선으로 연결하면서, 전체 간선 가중치의 합이 최소가 되도록 구성
• Prim 알고리즘과 달리 간선 중심(edge-based) 알고리즘
기본 아이디어
• 가중치가 가장 작은 간선부터 하나씩 선택하면서,
• 사이클이 생기지 않도록 주의하며
• $(|V| - 1)$개의 간선을 선택하면 완료
핵심 도구
• Greedy 방식으로 간선 선택
• 가중치 기준 정렬
• Union-Find (Disjoint Set) 자료구조로 사이클 판단
[ 시간복잡도 분석 (Analysis) ]
간선 정렬이 Kruskal의 핵심 시간 소모 요소: $W(m) \in \Theta(m \log m)$
• 여기서 $m$은 간선 수, $n$은 정점 수
[ 동작 예시 (How it works) ]
| 그림 | 내용 |
|---|---|
| 1단계 | 초기 그래프 주어짐 |
| 2단계 | 간선들을 가중치 기준으로 정렬(v1, v2)1, (v3, v5)2, (v1, v3)3, (v2, v3)3, (v3, v4)4, (v4, v5)5, (v2, v4)6 |
| 3단계 | 서로소 집합 초기화 $n(V) = N$ $n(E_T) = N - 1$(간선 수: 1부터 시작, N - 1까지) |
| 반복 | • 최소 가중치 간선 선택 • 사이클 없으면 추가, 사이클 생기면 무시 |
| 종료 | 모든 정점이 연결된 하나의 집합이 되면 완료 |
📌 아래 요약:
• 서로소 집합: $V = {V_1, V_2, …, V_5}$
• 예: ${v1}, {v2}, … ) → ( {v1, v2}$로 병합됨
[ 알고리즘 개요 (Overview) ]
F = ∅; // 간선 집합 초기화
create disjoint subsets of V, // 각 정점마다 하나씩 분리된 집합 생성
one for each vertex and
containing only that vertex;
sort the edges in E in nondecreasing order; // 간선을 오름차순으로 정렬
while (the instance is not solved){ // 해결되지 않았다면 반복
select next edge; // 간선 선택 (선택 절차)
if (the edge connects two vertices in disjoint subsets){ // 적합성 검사
merge the subsets;
add the edge to F; // 간선을 추가
}
if (all the subsets are merged) // 모든 정점이 하나의 집합이면
the instance is solved; // 해결 완료
}
//또는 간선의 수|F| = |V| - 1이 되면 종료해도 됨
[ Kruskal 의사코드 ]
void kruskal(int n, int m,
set_of_edges E,
set_of_edges& F)
{
index i, j;
set_pointer p, q;
edge e;
Sort the m edges in E by weight in nondecreasing order;
F = ∅;
initial(n); // n개의 분리된 집합 초기화
while (number of edges in F is less than n - 1){
e = edge with least weight not yet considered;
i, j = indices of vertices connected by e;
p = find(i);
q = find(j);
if (!equal(p, q)){
merge(p, q); // 집합 병합
add e to F;
}
}
}
다익스트라 알고리즘 SSP
[ 개요 ]
Y = {v₁};
F = ∅;
while (the instance is not solved) {
select a vertex v from V − Y, that has a
shortest path from v₁, using only vertices
in Y as intermediates;
add the new vertex v to Y;
add the edge (on the shortest path) that touches v to F;
if (Y == V)
the instance is solved;
}
[ 의사코드 ]
touch[i]
현재 v₁에서 vᵢ까지 가는 최단 경로 중, 마지막 간선 ⟨v, vᵢ⟩에서의 v의 인덱스(즉, vᵢ 바로 이전에 있는 정점 v)
prim 알고리즘에서 nearest와 유사
lenght[i]
v₁에서 vᵢ까지 Y의 정점들만 경유하여 도달하는현재까지의 최단 거리
prim 알고리즘에서 distance와 유사
void dijkstra (int n, const number W[][], set_of_edges& F)
{
index i, vnear;
edge e;
index touch[2..n];
number length[2..n];
F = ∅;
for (i = 2; i <= n; i++) {
touch[i] = 1; // 모든 정점 vᵢ에 대해 v₁에서 시작
length[i] = W[1][i]; // v₁에서 vᵢ로 가는 가중치로 초기화
}
repeat (n - 1 times) {
min = ∞;
for (i = 2; i <= n; i++) {
if (0 ≤ length[i] < min) {
min = length[i];
vnear = i; // 가장 가까운 정점 vnear 선택
}
}
e = edge from vertex touch[vnear] to vertex vnear;
add e to F; // 최단 경로 간선 추가
for (i = 2; i <= n; i++) {
if (length[vnear] + W[vnear][i] < length[i]) {
length[i] = length[vnear] + W[vnear][i]; // 거리 업데이트
touch[i] = vnear; // 경로 업데이트
}
}
length[vnear] = -1; // 선택 완료된 정점 표시
}
}
[ 시간복잡도 ]
2(n - 1)² ∈ θ(n²)
[ 예시 ]
스케줄링 SSP
[ 정의 ]
여러 작업(작업들)을 어떤 순서로 처리할지 결정하는 것
• 전체 처리 시간을 줄일 수 있고 기한(deadline)을 맞추거나 이익(profit)을 최대로 할 수 있음
• 종류: 마감기한이 있는 스케줄링, 마감기한이 없는 스케줄링
[ Scheduling (without deadlines) ]
1) 핵심 아이디어
서비스 시간이 짧은 작업부터 처리하면, 전체 시스템 체류 시간(total time in the system)이 최소화
2) 예시
• $t_1 = 5$, $t_2 = 10$, $t_3 = 4$
| Job | Time in the System (시스템 체류 시간) |
|---|---|
| 1 | 5 (서비스 시간) |
| 2 | 5 (대기) + 10 (서비스) = 15 |
| 3 | 5 (대기) + 10 (대기) + 4 (서비스) = 19 |
• 총합: $5 + (5 + 10) + (5 + 10 + 4) = 39$
• 가능한 스케줄 조합 & 총 체류 시간
| Schedule | Total Time in System |
|---|---|
| [1, 2, 3] | 39 |
| [1, 3, 2] | 33 |
| [2, 1, 3] | 44 |
| [2, 3, 1] | 43 |
| [3, 1, 2] | 32 (최적) |
| [3, 2, 1] | 37 |
3) 의사코드
sort the jobs by service time in nondecreasing order
while (the instance is not solved):
schedule the next job // selection + feasibility check
if (no more jobs):
instance is solved
4) 최적성 증명 (Proof of Optimality)
주장
전체 시스템 체류 시간을 최소화하는 유일한 스케줄은 작업들을 서비스 시간 기준으로 오름차순(non-decreasing order) 정렬하는 것
증명(귀류법)
| 구분 | 내용 |
|---|---|
| 가정 | • $t_i$: i번째 작업의 서비스 시간 $(1 ≤ i ≤ n−1)$ • 이 작업은 어떤 최적 스케줄(시스템 체류 시간을 최소화하는 스케줄)에서 실행된다고 가정 |
| 증명 | 해당 스케줄이 서비스 시간 기준으로 오름차순이라는 것을 보여야 한다 • 만약 작업들이 오름차순으로 정렬되지 않았다면, 적어도 하나의 인덱스 $i$가 존재해서: $t_i > t_{i+1}$ • 기존 스케줄에서 i번째 작업과 $(i+1)$번째 작업의 순서를 바꾼다: ‣ $(i+1)$번째 작업은 더 일찍 처리되므로 대기 시간이 줄어들어 시스템 체류 시간이 $t_i$만큼 감소 ‣ i번째 작업은 더 늦게 처리되므로 시스템 체류 시간이 $t_{i+1}$만큼 증가 • 따라서, 전체 시스템 체류 시간은 다음과 같다: $T’ = T + t_{i+1} - t_i$ |
| 결론 | $t_i > t_{i+1}$ 이므로 → $T’ < T$: 원래 스케줄보다 더 나은 스케줄이 존재하게 되어 모순 따라서, 최적 스케줄은 반드시 서비스 시간이 오름차순인 순서여야 한다 |
[ Scheduling with Deadlines ]
1) 핵심 아이디어
마감 기한 내에 수행되면 수익(profit)을 얻는 작업들 중에서 최대 수익을 얻을 수 있는 조합을 찾는다
참고
• Feasible: 조건을 만족해서 실제로 실행 가능한 상태다
• 마감기한이 있는 작업들 중 어떤 작업들을 선택해서, 마감기한을 지키면서 순서대로 처리할 수 있는 경우
2) 예제 (작업별 마감 기한과 수익)
| Job | Deadline | Profit |
|---|---|---|
| 1 | 2 | 30 |
| 2 | 1 | 35 |
| 3 | 2 | 25 |
| 4 | 1 | 40 |
Feasible한 스케줄 (가능한 순서) 예
| Schedule | Total Profit |
|---|---|
| [1, 3] | 55 |
| [2, 1] | 65 |
| [2, 3] | 60 |
| [3, 1] | 55 |
| [4, 1] | ✅ 70 (최적) |
| [4, 3] | 65 |
Unfeasible한 스케줄
• [1, 2] → deadline 만족하지 못함
3) 그리디 스케줄링 알고리즘
• 모든 가능한 스케줄을 고려하려면: 경우의 수가 많다 (Factorial time이 소요됨)
• 그리디(Greedy) 스케줄링 알고리즘을 설계하려면
작업들을 수익(profit) 기준으로 정렬, 작업을 하나씩 가능한 경우에 스케줄에 삽입
• 그리디 알고리즘 설계를 위한 정의
| Feasible Sequence(가능한 작업 순서) | Feasible Set (가능한 작업 집합) |
|---|---|
| [1, 3], [3, 1] | {1, 2} |
| [2, 1] | {2, 3} |
| [2, 3] | {1, 4} |
| [4, 1] | {2, 4} |
| [4, 3] | {3, 4} |
참고 집합의 순서가 달라도 profit이 달라지지는 않는다 → 이전만큼 엄청나게 중요하지는 않다
• 그리디 스케줄링 알고리즘의 목표
가능한 순서 중에서 총 수익이 최대가 되는 순서를 찾는다
👉 의미: optimal sequence (최적 순서)
👉 optimal set of jobs = 그 최적 순서에 포함된 작업들의 집합
4) 의사코드
Sort the jobs in nonincreasing order of profit
sort(jobs by profit in descending order)
S = ∅ // Initialize selected job set
while (there are jobs left to consider) {
job = select next job from the sorted list
if (S ∪ {job} is feasible) {
S = S ∪ {job} // Add job to schedule
}
if (no more jobs to consider) {
break // Problem instance is solved
}
}
return S // S is the set of scheduled jobs with maximum total profit
| Job | Deadline | Profit |
|---|---|---|
| 1 | 3 | 40 |
| 2 | 1 | 35 |
| 3 | 1 | 30 |
| 4 | 3 | 25 |
| 5 | 1 | 20 |
| 6 | 3 | 15 |
| 7 | 2 | 10 |
• S는 ∅로 시작함
• S = {1} → [1]은 가능하므로 선택됨
• S = {1, 2} → [2, 1]은 가능하므로 선택됨
• {1, 2, 3} → 불가능한 순서이므로 제외됨
→ 대신 {1, 2, 4}는 [2, 1, 4]가 가능하므로 선택됨
• {1, 2, 4, 5} → 불가능한 순서이므로 제외
• {1, 2, 4, 6} → 불가능
• {1, 2, 4, 7} → 불가능
최종 선택된 작업 집합: {2, 1, 4}
5) Identification of Feasibility (가능성 판단 기준)
S가 feasible(가능한 집합)이기 위한 조건:
S에 포함된 작업들을 마감기한 오름차순으로 정렬한 순서가 feasible한 경우에만 S는 feasible하다.
증명:
S가 feasible하다고 하자. 그렇다면 적어도 하나의 feasible한 순서가 존재한다.
job x가 job y보다 먼저 스케줄링되어 있고, job y의 마감기한이 더 이르다고 가정하자
이 두 작업의 순서를 바꾸어도 바꾼 순서도 여전히 feasible함
• job y는 더 빨리 시작하게 되므로 마감기한을 지킬 수 있고
• job x도 이전 시간대를 사용하므로 마감기한 내에 완료 가능
이러한 성질을 반복적으로 적용하여 Exchange Sort를 통해
정렬된 순서가 feasible하다면 전체도 feasible하다고 증명할 수 있음
결론적으로, 정렬된 순서가 feasible하면 → 해당 집합 S는 feasible하다.
Feasibility 판별 예시
• 집합 {1, 2, 4, 7}의 가능한 순서 중 하나가 [2, 7, 1, 4]라고 하자
• 각 작업의 마감기한을 해당 순서대로 표시하면: 1 2 3 3 (시간 슬롯)
• 총 4개의 작업을 3개의 시간 슬롯에 넣으려 하므로 불가능 (feasible하지 않음)
**문제 정의:**
각 작업은 마감기한 내에 완료되어야만 수익을 얻을 수 있다.
최대 수익을 얻을 수 있는 작업들의 스케줄을 결정하라.
**입력:**
n: 작업의 개수
deadline[i]: i번째 작업의 마감기한
작업들은 수익 기준으로 내림차순 정렬되어 있다고 가정
**출력:**
- 최대 수익을 내는 작업 순서 \( J \)
void schedule(int n, const int deadline[], sequence_of_integer& J) {
index i;
sequence_of_integer K;
J = [1];
for (i = 2; i <= n; ++i) {
K = J with i added according to nondecreasing values of deadline[i];
if (K is feasible)
J = K;
}
}
| Job | Deadline |
|---|---|
| 1 | 3 |
| 2 | 1 |
| 3 | 1 |
| 4 | 3 |
| 5 | 1 |
| 6 | 3 |
| 7 | 2 |
단계별 실행:
• J = [1]
• K = [2, 1] → feasible → J = [2, 1]
• K = [2, 3, 1] → not feasible → reject
• K = [2, 1, 4] → feasible → J = [2, 1, 4]
• K = [2, 5, 1, 4] → not feasible → reject
• K = [2, 1, 6, 4] → not feasible → reject
• K = [2, 7, 1, 4] → not feasible → reject
최종 결과:
$J = [2, 1, 4]$
[ 최악 시간 복잡도 (Worst-Case Time Complexity) ]
기본 연산
• 작업 정렬 시: 비교 필요
• 매 반복마다: $J + i$ 집합이 feasible한지 확인하는 비교 필요
• 입력 크기: $n$ 작업 수
• 정렬 시간: $\Theta(n \log n)$
• 반복문 내 비교: $i4$번째 루프에서 최대 $i-1$개의 비교
→ 합치면 $\sum_{i=2}^n [(i-1) + i] = n^2 - 1 \in \Theta(n^2)$
$W(n) \in \Theta(n^2)$
